- Index
-
Verification
Comparison with Pile Lateral Resistance from Plastic Deformation Theory
Ito and Matsui (1975)2 developed a method to estimate the lateral force acting on stabilizing piles in a slope, based on the theory of plastic deformation. The theoretical horizontal lateral force at a given depth (per unit width of slope) can be calculated for a given pile diameter, center-to-center spacing, and soil unit weight, and then integrated across the length of the pile intersected by the trial slip surface. The estimation of the lateral force is applicable to piles under the condition of restrained pile top.The following problem for comparison is described in the paper from Hassiotis et al. (1997)1, with further discussion and comparison by Hull and Poulos (1999)3, and is used to demonstrate the use of specifying a shear strength envelope for Pile reinforcements in MacSlope. It is not intended to serve as a verification of reported results, but as a comparison to understand the MacSlope implementation of pile shear resistance.
The slope considered is 13.7 m high at a slope angle of 30 deg, and consists of a uniform soil with γ = 19.63 kN/m3, Φ = 10 deg, and c = 23.94 kPa.
Hassiotis et al. used the friction circle method modified to include the stabilizing force provided by the piles, to examine the variation in factor of safety of the critical slip surface with distance from the toe of the slope to the row of piles. The reinforcing force provided by the piles is taken to act parallel to the slip surface at the intersection with the pile. The factor of safety for the unreinforced slope was reported as 1.08, with an improvement to 1.82 and 1.64 with a row of piles placed 13.7m and 23.1m from the toe respectively. The ratio of the clear distance between piles to the center-to-center spacing (D2/D1) used was 0.6.
In comparison, for the same slope Hull and Poulos reported the factor of safety as 1.12, with an improvement to 1.45 wth a row of piles placed 13.7m from the toe. Their analysis used a modified Bishop's Simplified method considering a shear force and bending moment generated from a boundary element analysis, acting at the pile intersection with the slip surface. They also note that the lateral pile force should act horizontally to be consistent with the plastic deformation theory formulation.
In this comparison, the pile reinforcement force is modeled using the Shear Strength from Envelope option, to represent the stabilizing lateral force reaction from the row of piles to the soil, calculated using the plastic deformation theory proposed by Ito and Matsui. Considering a pile diameter of 1.0m, the center-to-center spacing must be 2.5m (clear space of 1.5m between piles) to satisfy the given D2/D1 ratio of 0.6. For a pile length of 17m, the lateral force is estimated to be 72.4 kN/m at the pile head and 561.7 kN/m at the pile base, using equation (13) from Ito and Matsui.
Using the auto search, the factor of safety for the unreinforced slope is calculated as 1.109 and the critical slip surface is shown below.
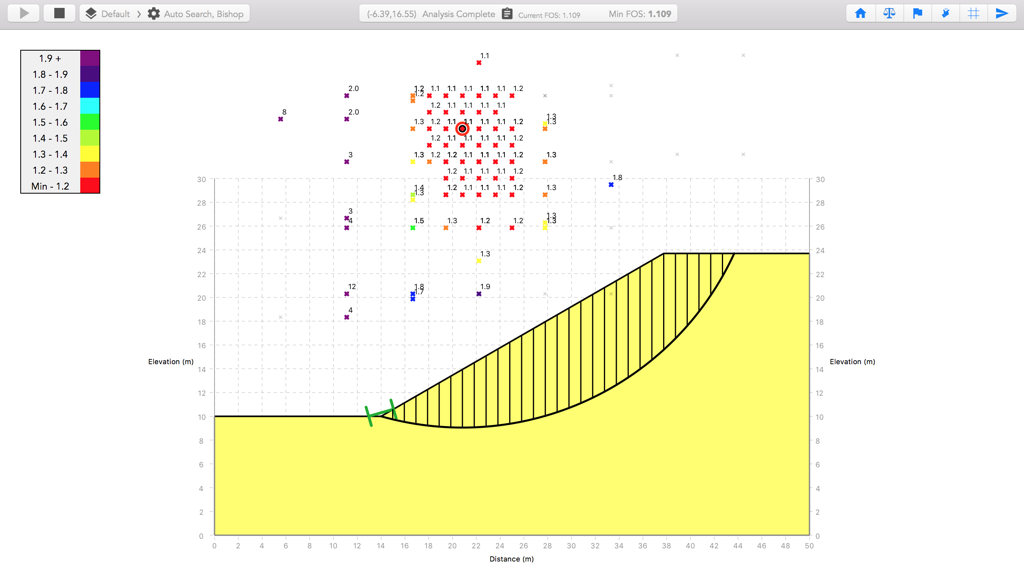
Although Hassiotis et al. propose the use of a reduced mobilized pile force depending on the global safety factor, it is understood the force Fp considered in their analysis is not factored by the global FOS, and acts parallel to the slip surface at the intesection with the pile. Therefore the Use Computed FOS option is disabled for the piles and the Force Inclination is set to 1.
The MacSlope factor of safety is calculated as 1.838 and 1.597 for piles placed at 13.7m and 23.1m from the toe respectively, using Bishop's Simplified method. Ranges are placed at the crest and toe of the slope to prevent possible failures that don't intersect the piles. The critical slip surfaces are shown below.
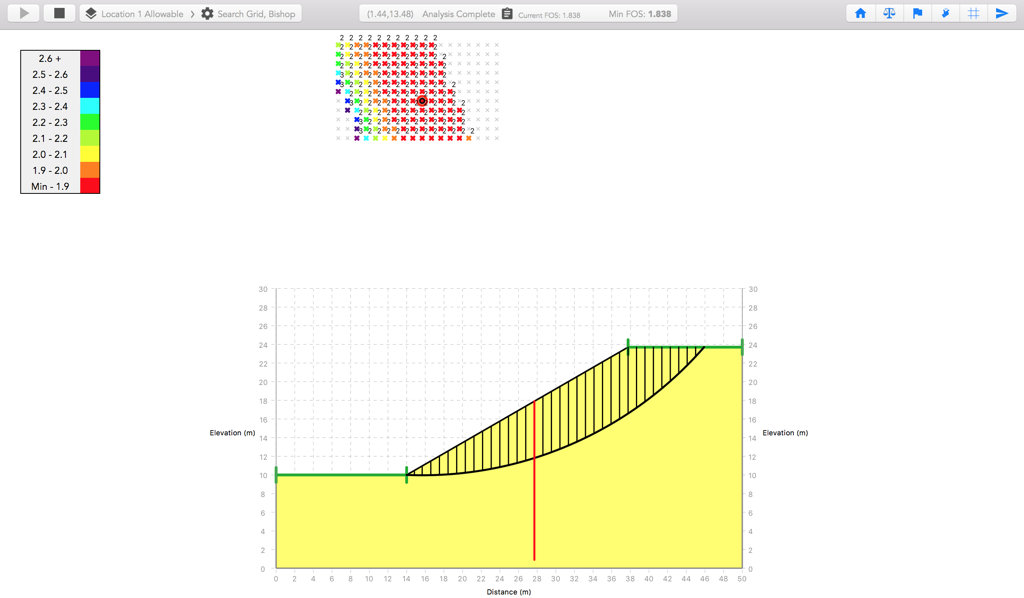
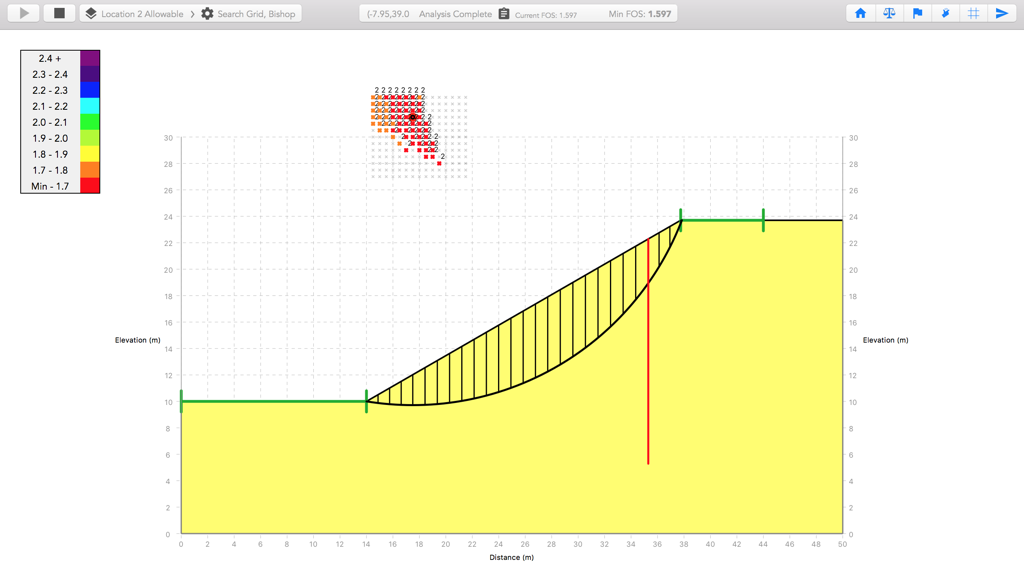
As noted by Hassiotis et al., when the lateral pile resistance is calculated from the plastic deformation theory where the soil is in a state of plastic equilibrium, it is appropriate to reduce the resistance by the computed FOS of the soil mass. Hull and Poulos note that the denominator in their factor of safety equation stays constant, indicating that moments from reinforcement forces are added to the resisting moment, and thus divided by the global FOS. When the Use Computed FOS option is enabled for the piles and the Force Inclination is set to 0 to act perpendicular (horizontally) to the pile, the calculated factor of safety is 1.522 for piles placed at 13.7m from the toe, which is similar to the result of 1.45 reported by Hull and Poulos. The difference (~5%) may be explained by their use of a slightly different lateral pressure distribution calculated by the boundary element method.
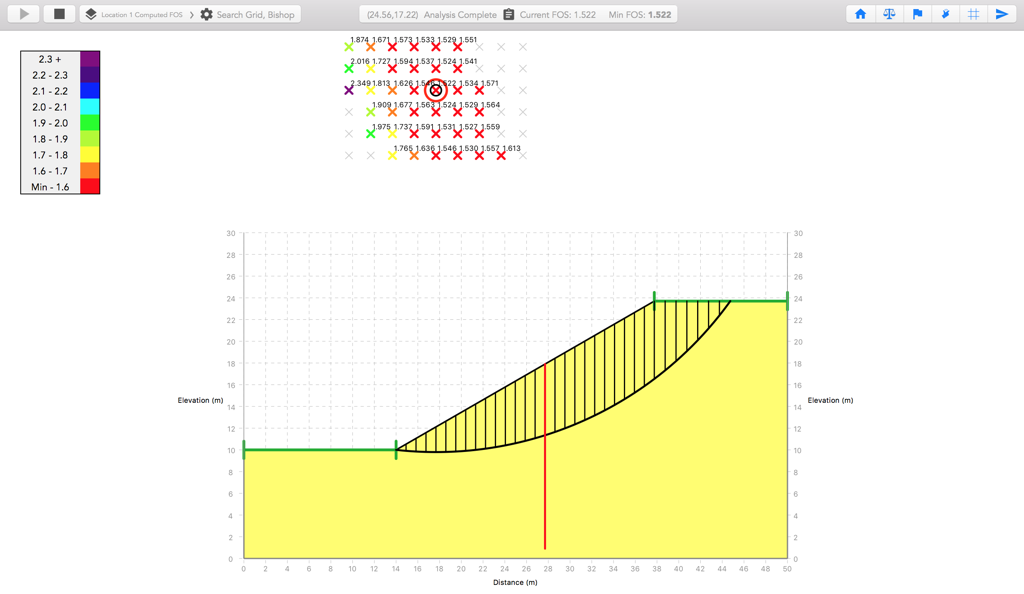
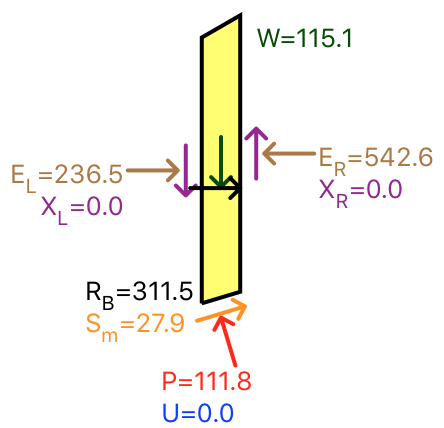
Inspecting the slice where the slip surface intersects the pile, we can check to see how the reinforcement force is modeled. The pile intersects the slip surface at a depth of 6.56m, which gives a lateral force per unit width slope of 72.4 kN/m + (6.56m/17m)*561.7 kN/m = 289.1 kN/m at that depth, while the lateral force at the top of the pile is 72.4 kN/m. Integrating the area under the pressure envelope gives us 6.43m*(72.4 kN/m + 0.5*(289.1 - 72.4) kN/m) = 1185.7 kN. Dividing by the pile center-to-center spacing and further by the computed FOS, we have 1185.7 kN / 2.5m / 1.522 = 311.6 kN/m. Comparing with the reinforcement force of noted in the free body diagram below, which is applied at the centroid of the envelope, we see the force is modeled as expected.
As can be seen by the range in factor of safety calculated between methods, significant care must be taken when specifying the parameters for pile reinforcement in MacSlope to ensure that the reinforcement force is modeled as expected. It should be noted that while limit equilibrium analysis of pile-reinforced slopes can be a useful tool to evaluate improvements to marginally stable slopes as well as expected design loads on piles, there are many other checks and considerations required for design.
Download the MacSlope file with the analysis results for this example here.
References
- Hassiotis, S., Chameau, J. L., and Gunaratne, M. (1997). Design method for stabilization of slopes with piles, Journal of Geotechnical and Geoenvironmental Engineering, 123(4), 314–323.
- Ito, T. Matsui, T (1975). Methods to estimate lateral force acting on stabilizing piles. Soils and Foundations, 15(4), 43-59.
- Hull T.S., Poulos H.G. Design method for stabilization of slopes with piles (discussion). Journal of Geotechnical and Geoenvironmental Engineering, ASCE 1999;125(10):911-3.